2524. Строки Фибоначчи
В математике
часто используются так называемые рекуррентные соотношения. Обычно с их помощью
задают числовые последовательности, однако они также могут применяться для
определения последовательностей строк.
Одним из
примеров строк, определяемых рекуррентными соотношениями, являются фибоначчиевы
строки. Они задаются следующим образом:
F0 = a,
F1 = b,
Fi = Fi - 2 + Fi - 1, i > 1
Первые семь фибоначчиевых
строк имеют следующий вид:
a,
b,
ab,
bab,
abbab,
bababbab,
abbabbababbab
Дима посещает
кружок олимпиадного программирования и интересуется алгоритмами на строках.
Недавно он узнал о фибоначчиевых строках и быстро заметил, что при увеличении
индекса i длина строки Fi растёт очень
быстро. Поэтому хранение всей строки целиком требует слишком много памяти. В
связи с этим Дима решил ограничиться задачей поиска отдельных символов.
Напишите
программу, которая определяет k-й символ строки Fn.
Вход. В первой строке задано число тестов t (1 ≤ t
≤ 100). В каждой из следующих t строк заданы два целых числа n и k (0 ≤ n ≤ 45, 1 ≤ k
≤ |Fn|), где |Fn| – длина строки Fn. Позиции символов в строке
нумеруются с единицы.
Выход. Выведите t строк. В каждой строке должен быть выведен ровно один символ – ответ на
соответствующий тест.
|
Пример
входа |
Пример
выхода |
40 11 13 2
7 7 |
a b a a |
РЕШЕНИЕ
рекурсия,
строки
Анализ алгоритма
Фибоначчиевы
строки определяются рекуррентно:
Fn = Fn–2 + Fn–1
Это означает,
что строка Fn состоит из
двух подряд идущих частей:
·
первых Fn–2
символов – это строка Fn–2,
·
следующих Fn–1
символов – это строка Fn–1.
Следовательно,
чтобы найти k-й символ строки Fn,
не нужно строить всю строку. Достаточно определить, в какой из двух частей он
находится.
Обозначим через
Fn(k) k-ый символ строки Fn.
Тогда:
·
если k ≤ |Fn–2|, то искомый символ находится в первой
части:
Fn(k) = Fn-2(k)
·
иначе (если k > |Fn–2|), символ лежит во второй части:
Fn(k) = Fn-1(k – |Fn–2|)
Таким образом, задача
сводится к поиску символа в строках с меньшими индексами.
Пример
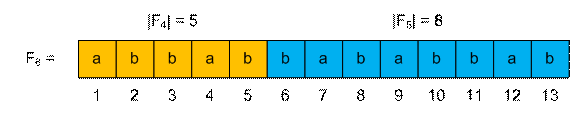
Рассмотрим строку F6, для которой имеют место
соотношения:
·
F6
= F4 + F5,
·
|F4| = 5, |F5| = 8
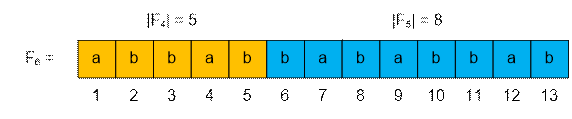
Вычислим F6(4). Поскольку k = 4 ≤ |F4| = 5, то F6(4)
= F4(4).
Вычислим F6(7). Поскольку k = 7 > |F4| = 5, то F6(7) = F5(7 – 5) = F5(2).
Реализация алгоритма
В массиве fib
хранятся
длины фибоначчиевых строк:
·
fib[i] содержит
длину строки Fi.
#define MAX 44
int fib[MAX] = {1, 1};
Функция solve
возвращает k-й
символ строки Fn, не строя саму строку
целиком.
char solve(int
n, int k)
{
Отдельно
обрабатываем базовые случаи n = 0 и n = 1.
if (n == 0) return 'a';
if (n == 1) return 'b';
Известно, что Fn = Fn - 2 + Fn - 1.
·
Если k ≤ Fn - 2, то k-ый символ лежит в строке Fn - 2.
·
Если k > Fn - 2, то k-ый символ лежит в строке Fn - 1. Однако его позиция смещается на длину
первой части, поэтому ищем символ с номером k – Fn - 2.
if (k <=
fib[n-2]) return solve(n - 2, k);
return
solve(n - 1, k - fib[n-2]);
}
Основная часть программы. Вычисляем
первые MAX чисел Фибоначчи.
for (i = 2; i <
MAX; i++)
fib[i] = fib[i-1] + fib[i-2];
Читаем количество тестов tests.
scanf("%d",&tests);
while (tests--)
{
Вычисляем и выводим ответ для каждого теста.
scanf("%d
%d",&n,&k);
printf("%c\n",solve(n,k));
}